|
RCI (順位相関係数)
RCIについて勉強しましょう。
RCIは私が利用している指標の一つですが、理解するのが非常に難しい指標でもあります。本日はRCIとは何であるのかその理解を中心にして説明したいと思います。
例えば貴方が競馬の予想をしたとします。5頭建てのレースで1位から5位までの順位を予想するとしましょう。
さあ予想しました。 レースが始まり結果がでました。
その結果あなたの予想と結果がどの程度当たっているかを得点化する方法はないだろうかと考えられたのがRCIです。
2つの相関関係がどの程度であるか(どのくらい当たっているか)を表す為の指標なのです。
ケース①
| 馬 |
予想 |
結果 |
|
| A |
1着 |
1着 |
|
| B |
2着 |
2着 |
|
| C |
3着 |
3着 |
|
| D |
4着 |
4着 |
|
| E |
5着 |
5着 |
|
あなたの予想と結果がぴったり一致しました。この場合の得点は100点満点となります。
ケース②
| 馬 |
予想 |
結果 |
|
| A |
1着 |
5着 |
|
| B |
2着 |
4着 |
|
| C |
3着 |
3着 |
|
| D |
4着 |
2着 |
|
| E |
5着 |
1着 |
|
こんどは、あなたの予想と結果がまったく逆になってしまいました。この時の得点は0点ではなくて-100点としましょう。
さあどうやって得点化しましょうかね。
そこで考えました。
予想と結果の順位の差を調べてみよう!
ケース①
| 馬 |
予想 |
結果 |
差 |
| A |
1着 |
1着 |
0 |
| B |
2着 |
2着 |
0 |
| C |
3着 |
3着 |
0 |
| D |
4着 |
4着 |
0 |
| E |
5着 |
5着 |
0 |
このようにすれば、差の合計が0であり、ピタリと当たっていることがわかります。
ケース②
| 馬 |
予想 |
結果 |
差 |
| A |
1着 |
5着 |
-4 |
| B |
2着 |
4着 |
-2 |
| C |
3着 |
3着 |
0 |
| D |
4着 |
2着 |
2 |
| E |
5着 |
1着 |
4 |
今度は大ハズレのケースですが、この差を合計してしまうと、同じく0になってしまします。これでは都合が悪いですね。そこで二乗して正数化することになりました。
ケース①
| 馬 |
予想 |
結果 |
差 |
差の2乗 |
| A |
1着 |
1着 |
0 |
0 |
| B |
2着 |
2着 |
0 |
0 |
| C |
3着 |
3着 |
0 |
0 |
| D |
4着 |
4着 |
0 |
0 |
| E |
5着 |
5着 |
0 |
0 |
差の2乗計 0
ケース②
| 馬 |
予想 |
結果 |
差 |
差の2乗 |
| A |
1着 |
5着 |
-4 |
16 |
| B |
2着 |
4着 |
-2 |
4 |
| C |
3着 |
3着 |
0 |
0 |
| D |
4着 |
2着 |
2 |
4 |
| E |
5着 |
1着 |
4 |
16 |
差の2乗計 40
ケース①の場合は差の2乗の合計が0で100点満点です。
ケース②の場合は差の2乗の合計が40で-100点となります。
ちょうど真中の20は0点になります。
これを株の値動きに利用しようとしたのです。
RCI (順位相関係数)
| RCI公式
:RCI = (1-d/F)×100 |
| RCI |
順位相関係数 |
| d |
期間内の差の2乗の合計 |
| F |
想定されるdの最大値の半分(ちょうど真中) |
株式市場で実際に応用してみましょう。
| 日付 |
終値 |
日付の順位 |
終値の順位 |
差の2乗 |
| 12/1 |
10300 |
1 |
3 |
4 |
| 12/2 |
10100 |
2 |
5 |
9 |
| 12/3 |
10400 |
3 |
2 |
1 |
| 12/4 |
10500 |
4 |
1 |
9 |
| 12/5 |
10200 |
5 |
4 |
1 |
差の2乗の合計(d)は24
想定されるdの最大値の半分(F)は20
RCI=(1-24/20)×100=-20
こんどは9日間のケースでやってみましょう。
9日間の場合の想定されるdの最大値は何になるのでしょうか?(大ハズレのケースで考えれば計算できます。)
では大ハズレのFを計算してみましょう。
| 日付の順位 |
終値の順位 |
差 |
差の2乗 |
| 1 |
9 |
-8 |
64 |
| 2 |
8 |
-6 |
36 |
| 3 |
7 |
-4 |
16 |
| 4 |
6 |
-2 |
4 |
| 5 |
5 |
0 |
0 |
| 6 |
4 |
2 |
4 |
| 7 |
3 |
4 |
16 |
| 8 |
2 |
6 |
36 |
| 9 |
1 |
8 |
64 |
差の2乗の合計(d)は240
想定されるdの最大値の半分(F)は120
| 日付 |
終値 |
日付の順位 |
終値の順位 |
差の2乗 |
| 12/15 |
10450 |
1 |
1 |
0 |
| 12/16 |
10240 |
2 |
7 |
25 |
| 12/17 |
10100 |
3 |
8 |
25 |
| 12/18 |
10100 |
4 |
8 |
16 |
| 12/19 |
10280 |
5 |
6 |
1 |
| 12/22 |
10310 |
6 |
5 |
1 |
| 12/24 |
10350 |
7 |
4 |
9 |
| 12/25 |
10390 |
8 |
3 |
25 |
| 12/26 |
10440 |
9 |
2 |
49 |
差の2乗の合計(d)は151
想定されるdの最大値の半分(F)は120(大ハズレのケースのdの半分)
RCI=(1-151/120)×100=-25.83
では実際にチャートをみてみましょう。(日経平均先物)
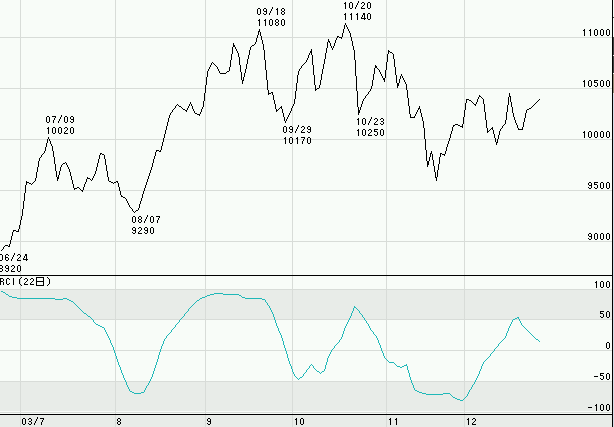
チャート提供 DreamVisor.com
日経平均先物の日足チャートです。
(まとめ)
・RCIは日付の順位と価格の順位の相関関係を数値化したオシレータである。
・0を中心として、-100~100の波動を描く。
・売買のタイミングを取るには適しません。
・短期線と長期線によるゴールデンクロス・デッドクロス等でタイミングを取ることもできます。
私はRCIが滑らかなラインを描くまで期間を延ばし、トレンドの方向を確認する為に利用しています。 RCIの向きと同一方向に株価が動くときは強気で相場を見ています
今回私が紹介した計算式は一般的な公式ではありません。しかし、RCIを感覚的に理解する為には想定されるdの最大値の半分が0になるといった理解が適していると判断しました。
一般的な公式は、
RCI={1-6d/N(N2-1)} Nは期間です。N2は期間の二乗です。
|

