| さて本日は、移動平均線について勉強したいと思います。
移動平均線の目的 : トレンドラインの確認
相場が上昇相場(ブル相場)なのか下降相場(ベア相場)なのか、保ち合い相場なのかを判断するのに利用します。
また、算定期間を変えた2種類の平均線を利用して、売買タイミングを取る方法もあります。しかしながら、平均線はトレンド転換シグナルが発生するタイミングが結果として遅れますので、トレンドの確認に利用することが望ましいといえます。
移動平均線の種類は多数存在しますが、ここでは単純移動平均線と指数平滑移動平均線の2つを取り上げることにします。
単純移動平均線(SMA:simple moving average)
| SMA公式
:y(t)=(Y(t)+Y(t-1)+Y(t-2)+.....Y(t-n+1)) / n |
| y(t) |
単純移動平均値(SMA) |
| Y(t) |
取引値
Y(0):当日引値 Y(-1):前日引値 Y(-n+1):平均期間(n)が5日間の場合、Y(-4)となる |
| n |
平均する期間 |
| 計算例 |
| Y(0) |
10,870円 |
当日の引値 |
| Y(-1) |
10,770円 |
1日前の引値 |
| Y(-2) |
10750円 |
2日前の引値 |
| Y(-3) |
10,800円 |
3日前の引値 |
| Y(-4) |
10720円 |
4日前の引値 |
| n |
5日間 |
平均算定期間 |
| y(t) |
(
10,870 + 10,770 + 10,750 + 10,800 + 10,720 ) / 5 = 10,782 |
指数平滑移動平均線(EMA:exponential moving average)
| EMA公式
: y(t)=y(t-1)+α(Y(t)-y(t-1)) |
| y(t) |
本日のEMA値 |
| y(t−1) |
昨日のEMA値 |
| Y(t) |
本日の引値(取引値) |
| α |
平滑化定数、0≦α≦1、α=2/(n+1) |
| n |
平均する期間 |
| |
|
| 計算例 |
| y(t−1) |
10,870円 |
昨日のEMA値 |
| Y(t) |
11,020円 |
本日の引値(取引値) |
| n |
5日間 |
平均する期間 |
| α |
2 / ( 5 + 1 ) = 0.33 |
| Y(t)-y(t-1) |
11,020 - 10,870 = 150 |
| y(t) |
10,870
+ 0.33 × 150 = 10,919 |
難しいですか?私は実際に計算してみてやっと理解できたのですが、皆さんがこの計算をやる必要はありません。しかし、是非覚えて行ってもらいたいことは、単純移動平均SMAより、指数平滑移動平均EMAの方がトレンド分析としては優秀であるということです。実際にグラフで比較して見ましょう。
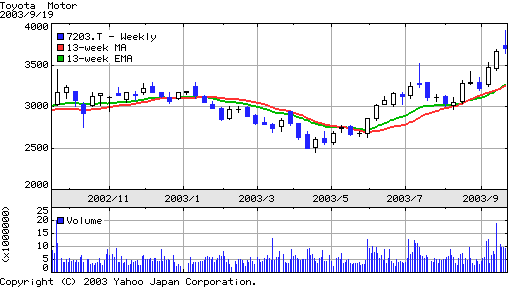
上のグラフはトヨタの週足チャートです。赤色のラインが単純移動平均(SMA)線です。一方緑色のラインが指数平滑移動平均(EMA)線です。どちらがトレンド分析に適しているかがわかりますよね。EMAの方がトレンドの転換が早く現れます。チャートソフトを持っている方でEMAが表示できる場合は、EMAを使用しましょう。上記のようにyahooファイナンスのグラフでも表示できますので、
皆さんのお持ちの銘柄で是非試してみてください。
指数平滑移動平均線(EMA)は優れものです。
単純な売買タイミングであれば、このEMAからでも可能です。上昇トレンドでは、EMAに近づいたら買いです。この平均線と株価を比べながら売買のタイミングを練習してみてください。(もちろん逆に動いたら、直ぐに清算してくださいね。)
|

